まえがき
ＷＴＡの硬式テニスの試合では時速200km（初速？）を超えるサーブを見ることは珍しくありません。
こんなサーブを見てミニテニスをやっている本人としてミニテニスでどの程度の高速サーブを打つことが出来るのか知りたくなり、試算してみました。
プロの打つ最速サーブは時速１２１ｋｍ
打撃速度の計算式
打球の速度を求めるのに次の算式を用います。
Vb=Vbo・ｅ + Vro(1 + e)
Vb：打球の速度(m/s) Vro：ラケットの速度(m/s) Vbo：飛球の速度(m/s) e：*1反発力係数：0.32(実測値)
サーブの際は、水平移動をしないボールを打つので、「Vbo：飛球の速度」はゼロになります。
従って、算式は次式に簡略化されます。
Vb=Vro(1 + e)=Vro*1.32
プロのスイング速度
ミニテニスのデーターがないのでＮｅｔで検索した硬式テニスの「テニスラケットの性能予測」に示されていたデーターを流用します。
これから、ラケットのスイング速度Vroを国内の或るトッププロの持つ秒速23.5m(時速84.6km)とします。
硬式テニスのラケットとミニテニスのラケットとでは長さが違いますのでミニテニスラケットのスイング速度に補正します。
上記のスイング速度を腕の長さ(上腕+前腕+手=70cm)を加えた、硬式テニスのラケット73.5cmとミニテニスのラケット57mmの長さ比で補正すると、ミニテニスラケットのスイング速度は次の通りになります。
Vro1=Vro＊R=23.5*（70+57-*115）/(70+73.5-15)≒20.5m/s≒74km/h
＊１：トップフレームから15cmのところをスイートスポットとします。
ボールの反発係数
(1)ミニテニスのルールから求める反発係数(e)は、０．６０～０．６６。平均値で０．６３
ミニテニスのルールには、床面に１５０cｍの高さから落としたボールは５５～６５cmの高さに弾むこととありますから
ミニテニスで言う反発係数は次のようになります。
反発係数(e)=(2*9.8*(0.55(0.65)))＾0.5/(2*9.8*1.5)＾0.5=0.60～0.66
(2)実測値で求める反発係数(e)は、
①ラケット面に１５０cmの高さからボールを落とした時の反発係数(e)は、０．６４
反発係数(e)=(2*9.8**10.62）＾0.5/(2*9.8*1.5)＾0.5=0.64 ＊1：データー数(N)=10の平均値。気温=20℃
②フローリングに１５０cmの高さからボールを落とした時の反発係数(e)は、０．６０
反発係数(e)=(2*9.8**20.55）＾0.5/(2*9.8*1.5)＾0.5=0.60 ＊2：データー数(N)=10の平均値。気温=20℃
これらのテスト条件でのボールの衝突速度は、5.4m/sec(19.5km/hr)と、実際のサーブやレシーブの際の衝突速度に比べて、はるかに遅いから、速い時の反発係数はこの値より小さくなると言われています。
尚、この傾向は、硬式テニスの調査（衝突速度が7m/secの時の反発係数が0.73～0.76の場合、衝突速度が速くなるに従い反発係数が小さくなる）で実証されています。
ボールの反発力係数
先に、ボールの弾みやすさの評価項目として一般的な「反発係数」を調べましたが、ラケットメーカー等の評価には「反発力係数」を使用しているらしいので、反発力係数を使用することにします。
ある研究者の研究結果にもとずく反発係数(ep)と反発力係数(e)の比率から反発力係数を換算します。
R=e/ep=0.51 とすると、求める反発力係数(e)は、 e=R*ep=0.51*ep より、次のようになります。
①ラケット面にボールを落とした時の反発係数は0.64だから、前式より、求める反発力係数(e)は、0.32
②フローリングにボールを落とした時の反発係数は0.6だから、前式より、求める反発力係数(e)は、0.3
★反発力係数とは：吊るしたラケットに水平方向にボールを衝突させたとき、衝突直前と直後の速度から反発力係数を求めます。これに対する反発係数は、水平に固定したラケット面にある高さから落としたボールがどれくらい跳ね返ったから求めます。反発力係数の方が実際に近い測定法だと考えられます。
プロの最速サーブ：推定値
以上より、最速サーブの初速度Vbは次の通りになります。
Vb=Vro1(1 + e)=20.5*(1+0.32)=20.5＊1.32≒27m/s≒97km/h
この初速でフラットサーブ・ドライブサーブ・スライスサーブをした時の速度と時間をシュミレーションしました。
| 種類 | 初速度 (m/s) |
平均速度 (m/s) |
終速度 (m/s) |
滞空時間 (s/秒) |
回転数 (回/分) |
打出し角度 (度) |
打出し高さ (m) |
飛距離 (m) |
| フラットサーブ | 27 | 11.3 | 7.7 | 1.17 | 0 | 16.6 | 0.84 | 13.4 |
| ドライブサーブ－１ | 27 | 11.3 | 7.7 | 1.19 | 12 | 17 | 0.84 | 13.4 |
| ドライブサーブー２ | 35 | 17.3 | 13.4 | 0.78 | 50 | 7.3 | 0.84 | 13.4 |
| スライスサーブ | 27 | 17.3 | 12.0 | 0.78 | 15 | 6 | 0.84 | 13.4 |
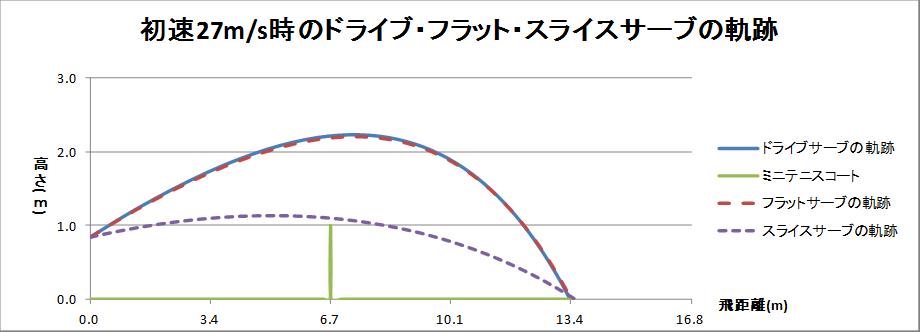
結果、初速27m/sのフラットサーブとドライブサーブとの間に有意差は見られませんが、スライスサーブとの間には平均速度が遅かったり、到達時間が長かったりする等有意差があります。
ただ、フラットサーブとスライスサーブでは初速27m/secは初速の最大値ではありますが、ドライブサーブでは打てるのであれば初速はドライブサーブ-2の初速35m/sでも70m/sでもラインアウトせずに打つことが可能です。
シュミレーション条件として、気温２０℃、風のない環境、空気抵抗はレイノルズ数に反比例、ボールの回転数は不変、とします。
サーブの最大初速：時速１６２km
身体能力を無視して飛距離１３．４mをサーブをする時のドライブサーブとフラットサーブの限界速度を試算しました。
ちなみに、硬式テニスの一般プレーヤーの初速は25m/s、トッププレーヤーの初速は35m/sらしいです。
結果、
①ドライブサーブもスライスサーブもボールが無回転ならば、フラットサーブと同じ結果になります。
②フラットサーブの場合、ドライブサーブと同じスイング速度で打つとラインオーバーしてしまうのでスイング速度(球速)を落とさざるを得なくなるとともに、滞空時間も長くなっています。
③スライスサーブはボールの回転が速い程揚力が働いて飛距離が長くなる性質がありますので、ボールの自重に相当する揚力が働く回転をボールに掛ければボールは落ちずに水平移動することになります。
スライスは浮き上らない程度の回転のバックスピンの掛かったゆっくり降下するサーブなので、ボール自重より小さい2/3～1/3揚力の働く毎分185回転を掛けた時の、初速は28m/s程になります。
| 項目 | 単位 | ドライブサーブ | フラットサーブ | スライスサーブ |
| スイング速度 | m/s(km/h） | 34.0(122.4） | 26.5(95.4) | 21.2(76.4) |
| 最大初速 | m/s(km/h） | 45.0(162) | 35（126） | 28(100.8) |
| 最大平均球速 | m/s(km/h) | 33.2(155) | 17.7(93) | 12.7(45.7) |
| 最大終速 | m/s(km/h) | 21.4(146) | 10.0(27.3) | 7.6(27.4) |
| 滞空時間 | s(秒) | 0.4 | 0.75 | 1.1 |
| 打出し角度 | 度 | 7.5 | 5 | 5.7 |
| 打出し高さ | m 腰の高さ | 0.84 | 0.84 | 0.84 |
| ボール回転数 | 回転/秒（回転/分） | 9(540)一定 | 0 | 3.1（185)一定 |
・反発力係数(e)はラケット面の係数０．３２を使用する。
・風の抵抗有り
・ボールがネットギリギリ(高さ106cm)を通過する高さ
